

This is not very difficult combinatorial proof of what you call the general version of inclusion/exclusion and is built on not more than one very simple lemma. The inclusion-exclusion principle, is among the most basic techniques of combinatorics. For example, for the three subsets, , and of, the following table summarizes the terms appearing the sum. With odd cardinality equals the number of subsets with even cardinality. The principle of inclusion-exclusion was used by Nicholas Bernoulli to solve the recontres problem of finding the number of derangements (Bhatnagar 1995, p. This is true because a case in which exactly $m$ of the conditions are fulfilled is counted $\binom mk$ times in $a_k$ and thus contributes Although the proof seems very exciting, I am confused because what the author has proved is 1 1 from. A set is a collection of related items, such as dog owners, or students in a. 12109 Heritage Park Circle Silver Spring MD 20906 email: URL:FebruThere is a marvelous counting formula based on a collection of observations called the principle of inclusion-exclusion. This proves the principle of inclusion-exclusion. In order to explain the inclusion-exclusion principle, we first need to cover some basic set theory. The Inclusion-Exclusion Principle Gary D. How many solutions does the equation have if all variables are positive integers 4. Therefore, each element in the union is counted exactly once by the expression on the right-hand side of the equation. When skillfully applied, this principle has yielded the solution to many a combinatorial problem. The inclusionexclusion principle is a well-known property in probability theory, and is instrumental in some computational problems such as the evaluation of. Which solution is correct to this question: find the number of different sequences (x1,x2,x3,x4,x5) with following rules. Ways to fulfill exactly $j$ of the conditions. 1 ( r 0) ( r 1) ( r 2) + ( r 3) + ( 1) r + 1 ( r r). 263-266.In answers to combinatorial questions, I sometimes use the fact that if there are $a_k$ ways to choose $k$ out of $n$ conditions and fulfill them, then there are RIEČAN, B.: A descriptive definition of the probability on intuitionistic fuzzy sets, in: Proc. Štépnička, et al., eds.), Universitas Ostraviensis, Ostrava, 2007, pp.

There is only one element in the intersection of all. The three-way intersections have 2 elements each. The pair-wise intersections have 5 elements each. RIEČAN, B.: M-probability theory on IF-events, in: New Dimensions in Fuzzy Logic and Related Technologies, Proc. Inclusion/Exclusion with 4 Sets Suppose you are using the inclusion-exclusion principle to compute the number of elements in the union of four sets. KUKOVÁ, M.: The Inclusion-Exclusion Principle for IF-events, Inform. KELEMENOVÁ, J.: The inclusion-exclusion principle in semigroups, in: Recent Advances in Fuzzy Sets, IF-Sets, Generalized Nets and Related Topics, Vol. 10.1016/j.ins.2010.10.003 Search in Google Scholar Thus, we have just proved the principle of inclusion and exclusion. GRZEGORZEWSKI, P.: The inclusion-exclusion principle for IF-events, Inform. By the inclusion-exclusion principle the number of onto functions from a set with six. What we have basically done is (1) counted all of A, (2).
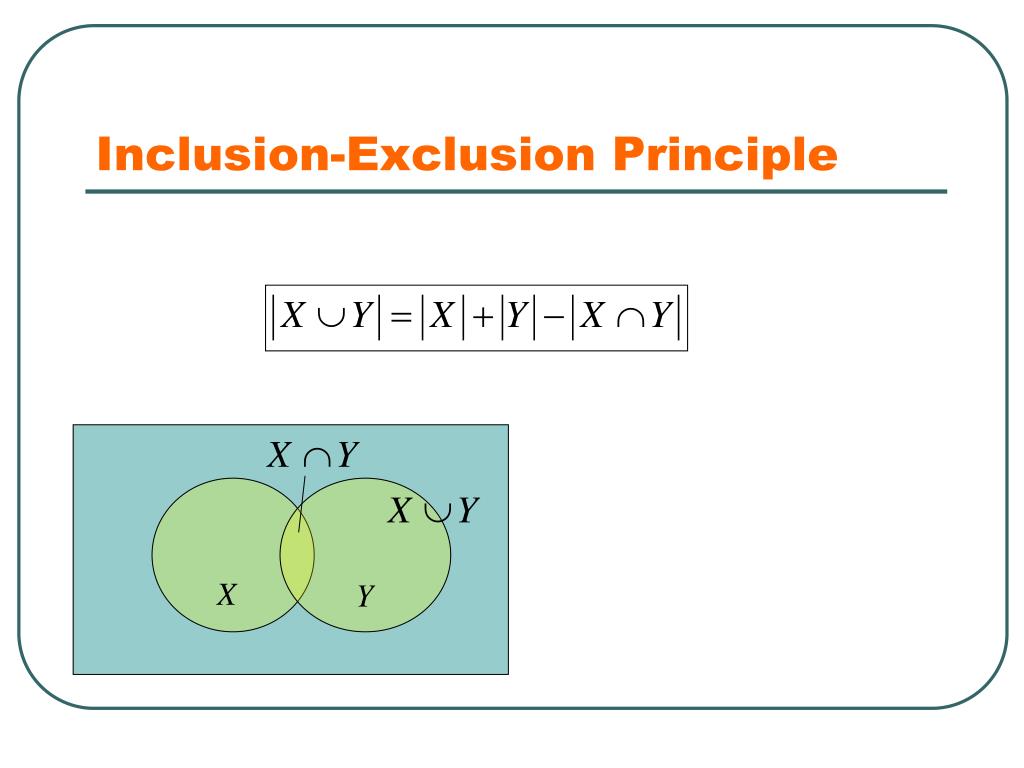
CIUNGU, L.: The inclusion-exclusion principle for IF-states, Inform. The function is onto if none of the properties P1, P2, and P3 hold. We have talked about the principle of inclusion-exclusion already: Acup B A+B-Acap B. WILF ’09, Palermo, Italy, Lecture Notes in Comput. CIUNGU, L.-RIEČAN, B.: General form of probabilities on IF-sets, in: Proc. In this paper we generalize (a) and(b) to the case where 1,, r are subsets of some countable but isolated set.


 0 kommentar(er)
0 kommentar(er)
